魏尔斯特拉斯函数

魏尔斯特拉斯函数（Weierstrass function）是一类处处连续而处处不可导的实值函数。魏尔斯特拉斯函数是一种无法用笔画出任何一部分的函数，因为每一点的导数都不存在，画的人无法知道每一点该朝哪个方向画。魏尔斯特拉斯函数的每一点的斜率也是不存在的。魏尔斯特拉斯函数得名于十九世纪的德国数学家卡尔·魏尔斯特拉斯。

魏尔斯特拉斯的原作中给出的构造是：

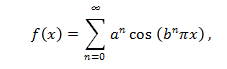
其中0<a<1，b为正奇数，使得

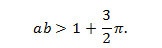
这个函数以及它处处连续而又处处不可导的证明，首次出现在1872年7月18日魏尔斯特拉斯在普鲁士科学院出版的一篇论文中。

证明这个函数处处连续并不困难。由于无穷级数的每一个函数项

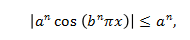
而正项级数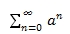是收敛的，由比较审敛法可以知道原级数一致收敛。又每一个函数项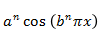都是R上的连续函数，所以级数的和f(x)也是R上的连续函数.

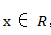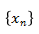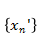证明这个函数处处不可导的思路是：对任意给定的点，找出趋于x的两组不同的数列和，使得

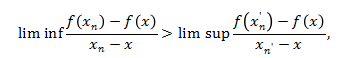
即说明f(x)在点X不可导。

区间[-2,2]上的魏尔斯特拉斯的图形如下：

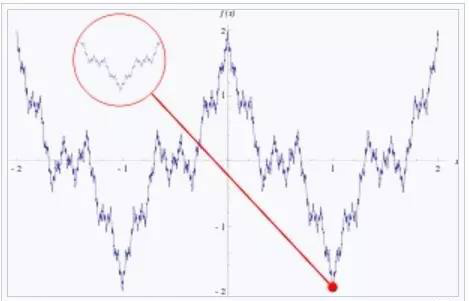
该函数也具有分形的特性：某些部分与整体自相似，曲线在平面有界区域内但长度为无穷。